![]()
ESM2 second year internship
Computation of “Boundary Layers” with FLUENT
SKODA Research -Fluid Department-, PLZEN
Table of Contents
1 Introduction........................................................................................................... 4
1.1 Skoda research................................................................................................. 4
1.2 Concept of boundary layer............................................................................... 4
2 Theoretical study of boundary layers.................................................................... 4
2.1 Laminar boundary layer.................................................................................... 4
2.1.1 Experimental description............................................................................................................... 4
2.1.2 Shape of the experimental laminar flow....................................................................................... 4
2.1.3 Analytical solution......................................................................................................................... 4
2.2 Turbulent boundary layer................................................................................. 5
2.2.1 Experimental description, turbulent transition........................................................................... 5
2.2.2 Shape of the experimental turbulent flow................................................................................... 5
2.2.3 Empirical solution........................................................................................................................... 5
3 Computation of boundary layers with FLUENT................................................. 6
3.1 Basics about FLUENT (from FLUENT 5 User’s Guide)................................ 6
3.1.1 Overview.......................................................................................................................................... 6
3.1.1.1 Wall Functions & Near-Wall Model Approaches................................................................ 6
3.1.1.2 Wall Functions........................................................................................................................... 7
·Overview of the standard wall functions........................................................................................... 7
·Limitations of the Wall Function Approach..................................................................................... 8
3.1.1.3 Two-Layer Zonal Model........................................................................................................... 8
3.1.1.4 Different Turbulence Models................................................................................................... 9
·The Spalart-Allmaras Model................................................................................................................ 9
·The Standard k-e Model....................................................................................................................... 9
·The Reynolds Stress Model................................................................................................................ 9
3.1.2 Grid Considerations for Turbulent Flow Simulations............................................................. 10
3.1.2.1 Near-Wall Mesh Guidelines for the Two-Layer Zonal Model.......................................... 10
3.2 Case of the “flat plate”................................................................................... 10
3.2.1 Theoretical study......................................................................................................................... 10
3.2.1.1 Determination of the flow & grid parameters....................................................................... 10
3.2.1.2 Choice of the Uo & flow characteristics................................................................................ 11
3.2.1.3 Building the grids..................................................................................................................... 11
·First grid................................................................................................................................................ 11
·Second grid.......................................................................................................................................... 13
3.2.1.4 Mesh considerations............................................................................................................... 15
3.2.2 Laminar computation................................................................................................................... 15
3.2.2.1 Computation setup.................................................................................................................. 15
3.2.2.2 First grid.................................................................................................................................... 15
3.2.2.3 Second grid............................................................................................................................... 18
3.2.2.4 Conclusions.............................................................................................................................. 19
3.2.3 Turbulent computation................................................................................................................ 19
3.2.3.1 Computation adjustments....................................................................................................... 19
3.2.3.2 First grid.................................................................................................................................... 19
·Spalart-Allmaras model....................................................................................................................... 19
·k-e model............................................................................................................................................... 21
·Reynolds stress model....................................................................................................................... 24
3.2.3.3 Second grid............................................................................................................................... 25
·Spalart-Allmaras model....................................................................................................................... 25
·k-e model............................................................................................................................................... 25
·Reynolds stress model....................................................................................................................... 26
3.2.4 Conclusions.................................................................................................................................. 28
4 Appendix............................................................................................................... 29
4.1 First Grid.......................................................................................................... 29
4.2 Second Grid...................................................................................................... 29
Thanks..................................................................................................................... 29
Bibliography:................................................................................................................ 31
SKODA VYZKUM incorporates a number of mutually interconnected theoretical and experimental laboratories, with the main activities in research, development, testing and consultancy related to advanced materials and technologies, and specific fields of interest in mechanical engineering, electrical engineering and power generation technology.
The scientific and engineering capabilities of the company are used to solve problems of top priority in modern technology, particularly:
- Improvements of product parameters
- Improvements of operational reliability and
service life of products
- Decreasing costs
- Decreasing the power requirements of the manufacturing
process
The concept of “boundary layer” is very useful and essential to succeed in computation of external flows around objects.
It was introduce in 1904 by Ludwig PRANDTL, following the idea that the viscous effects “near the walls” could be reduce to a thin layer on the surface of the body.
Outside this layer, the fluid behaves like if it was unviscid, and simpler models - like the unviscid or the potential ones - can be used.
As the viscous effects produce large gradients they cannot be occulted.
The concept of “two zonal layer” is useful because on the one hand it confine the laminar (viscous) effects in a thin layer and on the other hand it contributes to accurate the computation of the flow in comparison to the unviscid model.
Currently, these models are the only way to solve external flow problems – which are otherwise still unsolvable.
This model of two layers boundary flow has been studied and experimented for a long time, and the analytical and empirical models, which were build, seem to work quite well.
In this report, I will try to study how fluent deals with these boundary layers, and if the results are compatible with the analytical and empirical formulas.
Eventually, I will try to give a good way to take these boundary layers in account in a computation.
To verify the accuracy of computation with FLUENT about the boundary layers, we will begin with the simple case of the “flat plate”.
We are considering the flow of air (considered as a laminar incompressible fluid) over a flat plate. There are any pressure gradient and any heat transfers.
This situation is ideal but admits analytical solutions, which will be easy to compare with the computation.

![]() : Velocity
vector in the boundary layer
: Velocity
vector in the boundary layer
The solution of such a flow is given by the Navier-Stockes equations. But for steady two-dimensional flow with negligible gravitational effects and making some hypothesis about the velocity field, these equations can be simplify to the others called the PRANDTL equations, for which is now possible to find analytical solutions…(which won’t be demonstrated).
Assuming that the thickness of the boundary layer is given by d which represent the ordinate when the velocity “u” reach 99% of the velocity inlet: “Uo”, the solutions for a laminar flow over a flat plate were given by BLASIUS:


With: n = 1.46 10-5 SI: kinematics viscosity of air
Rex = U´x/n: “x-Reynolds” number
The experience considered is the same than which is described in 2.1), but now we consider the fluid as a turbulent one.
In fact the Reynolds number is growing along the plate proportionally to the x coordinate. And after a critical value of the Rex, which depends on several parameters but that we can estimate between 105 and 3.106 the flow become turbulent, modifying appreciably the velocity field.
The transition from laminar to turbulent flow also involves a noticeable change in the shape of the boundary layer velocity profile. The turbulent profiles are flatter, have a larger velocity gradient at the wall, and produce a larger boundary layer thickness than do the laminar profiles.

We can notice that after the transition region which can be supposed to occur when the Rex reach 105 we should observe a “bump” in the shape of the boundary layer.
The thickness of the laminar sublayer decreases and become very thin. In the turbulent flow, the velocity field is modified.
It will be interesting to compare these characteristics with the computed solution…
As there are no exact analytical solutions for the turbulent boundary layer, we would compare our computation to semi-empirical formulas, which proved their effectiveness through the experiment:


These formulas will be used after the transition area. The laminar ones remaining true before.
Before starting to compute, or even build a mesh for our computation, it is necessary to understand how FLUENT deals with these boundary layers.
Turbulent flows are significantly affected by the presence of walls. Obviously, the mean velocity field is affected through the no-slip condition that has to be satisfied at the wall.
However, the turbulence is also changed by the presence of the wall in non-trivial ways. Very close to the wall, viscous damping reduces the tangential velocity fluctuations, while kinematics blocking reduces the normal fluctuations.
Toward the outer part of the near-wall region, however, the turbulence is rapidly augmented by the production of turbulent kinetic energy due to the large gradients in mean velocity.
The near-wall modeling significantly impacts the fidelity of numerical solutions, inasmuch as walls are the main source of mean vorticity and turbulence. After all, it is in the near-wall region that the solution variables change with large gradients, and the momentum and other scalar transports occur most vigorously. Therefore, accurate representation of the flow in the near-wall region determines successful predictions of wall-bounded turbulent flows.
The K-E and RSM turbulence models are primarily valid for turbulent core flows (i.e., the flow in the regions somewhat far from walls). Consideration therefore needs to be given as to how to make these models suitable for wall-bounded flows. The Spalart-Allmaras model was designed to be applied throughout the boundary layer, provided that the near-wall mesh resolution is sufficient.
Numerous experiments have shown that the near-wall region can be largely subdivided into three layers. In the innermost layer, called the “viscous sublayer”, the flow is almost laminar-like, and the (molecular) viscosity plays a dominant role in momentum and heat or mass transfer. In the outer layer, called the “fully turbulent” layer, turbulence plays a major role. Finally, there is an interim region. Between the “viscous sublayer” and the “fully turbulent” layer where the effects of molecular viscosity and turbulence are equally important.
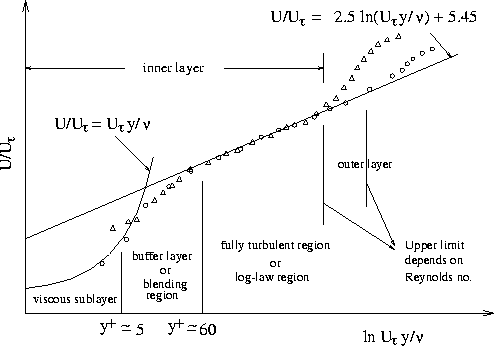
Figure 1: Subdivisions of the Near-Wall Region, plotted in semi-log coordinates.
There are two approaches to modeling the near-wall region. In one approach, the viscosity-affected, inner region (viscous sublayer and buffer layer) is not resolved. Instead, semi-empirical formulas called “wall functions” are used to bridge the viscosity-affected region between the wall and the fully turbulent region. The use of wall functions obviates the need to modify the turbulence models to account for the presence of the wall.
In another approach, the turbulence models are modified to enable the viscosity-affected region to be resolved with a mesh all the way to the wall, including the viscous sublayer. For purposes of discussion, this will be termed the “near-wall modeling” approach. These two approaches are depicted schematically in Figure 2.

Figure 2: Near-Wall Treatments in FLUENT
In high-Reynolds-number flows, the wall function approach substantially saves computational resources, because the viscosity-affected near-wall region, in which the solution variables change most rapidly, does not need to be resolved. The wall function approach is popular because it is economical, robust, and reasonably accurate. It is a practical option for the near-wall treatments for industrial flow simulations.
The wall function approach, however, is inadequate in situations where the low-Reynolds-number effects are pervasive in the flow domain in question, and the hypotheses underlying the wall functions cease to be valid. Such situations require near-wall models that are valid in the viscosity-affected region and accordingly integrable all the way to the wall.
FLUENT provides both the wall function approach and the near-wall modeling approach.
Wall functions are a collection of semi-empirical formulas and functions that in effect “bridge” or “link” the solution variables at the near-wall cells and the corresponding quantities on the wall. The wall functions comprise:
-Laws-of-the-wall for mean velocity and temperature (or other scalars)
- Formulas for near-wall turbulent quantities
The logarithmic law for mean velocity is known to be valid for:
In FLUENT, the log-law is employed when y*> 11.225.
When the mesh is such that y*< 11.225 at the wall-adjacent cells, FLUENT applies the laminar stress-strain relationship
In short, using the wall functions, the velocity speed at wall-adjacent cells are determined with:
- The log law if the parameter y* is higher than 11.225
- The laminar formula if the parameter y* is inferior than 11.225
The standard wall functions give reasonably accurate predictions for the majority of high-Reynolds-number, wall-bounded flows.
However, the wall function approach becomes less reliable when the flow conditions depart too much from the ideal conditions underlying the wall functions. Examples are as follows:
- Pervasive low-Reynolds-number or near-wall effects (e.g., flow through a small gap or highly viscous, low-velocity fluid flow)
- Massive transpiration through the wall (blowing/suction)
- Severe pressure gradients leading to boundary layer separations…
If any of the items listed above is a prevailing feature of the flow you are modeling, and if it is considered critically important to capture that feature for the success of your simulation, you must employ the near-wall modeling approach. FLUENT provides the two-layer zonal model for such situations. This two-layer model can be used with the three k-e models and the RSM.
Taking this conclusion into consideration, it is clearly understood that we will not use the wall functions for our study but we rather will use the Two-Layer Zonal Model…
In FLUENT's near-wall model, the wall functions are completely abandoned in favor of resolving the viscosity-affected near-wall region all the way to the viscous sublayer. In the two-layer model, the whole domain is subdivided into a viscosity-affected region and a fully turbulent region. The demarcation of the two regions is determined by a wall-distance-based, turbulent Reynolds number, Rey, defined as:
 (7)
(7)
Where “y” is the normal distance from the wall at the cell centers. In FLUENT, y is interpreted as the distance to the nearest wall:
![]() (8)
(8)
Where r is the position vector at the field point, and rw is the position vector on the wall boundary.Gw is the union of all the wall boundaries involved. This interpretation allows y to be uniquely defined in flow domains of complex shape involving multiple walls. Furthermore, y defined in this way is independent of the mesh topology used, and is definable even on unstructured meshes.
In the fully turbulent region (Rey > 200), the k-e models or the RSM are employed.
In the viscosity-affected near-wall region (Rey < 200), the one-equation model of Wolfstein is employed. In the one-equation model, the momentum equations and the k equation are retained. However, the turbulent viscosity,mt, is computed from:
![]() (9)
(9)
The field is computed from
![]() (10)
(10)
The length scales that appear in Equations 8 and 9 are computed from
 (11)
(11)
![]() (12)
(12)
If the whole flow domain is inside the viscosity-affected region (Rey < 200), is not obtained by solving its transport equation; it is instead obtained algebraically from the formula in Equation 10.
The constants in the length scale formulas, Equations 11 and 12, are taken from Chen and Patel:
![]()
The Spalart-Allmaras model is a relatively simple one-equation model that solves a modeled transport equation for the kinematics eddy (turbulent) viscosity. This embodies a relatively new class of one-equation model in which it is not necessary to calculate a length scale related to the local shear layer thickness. The Spalart-Allmaras model was designed specifically for aerospace applications involving wall-bounded flows and has been shown to give good results for boundary layers subjected to adverse pressure gradients. It is also gaining popularity for turbomachinery applications.
In its original form, the Spalart-Allmaras model is effectively a low-Reynolds-number model, requiring the viscous-affected region of the boundary layer to be properly resolved. In FLUENT, however, the Spalart-Allmaras model has been implemented to use wall functions when the mesh resolution is not sufficiently fine. This might make it the best choice for relatively crude simulations on coarse meshes where accurate turbulent flow computations are not critical. Furthermore, the near-wall gradients of the transported variable in the model are much smaller than the gradients of the transported variables in the k-E models. This might make the model less sensitive to numerical error when non-layered meshes are used near walls.
On a cautionary note, however, the Spalart-Allmaras model is still relatively new, and no claim is made regarding its suitability to all types of complex engineering flows. For instance, it cannot be relied on to predict the decay of homogeneous, isotropic turbulence. Furthermore, one-equation models are often criticized for their inability to rapidly accommodate changes in length scale, such as might be necessary when the flow changes abruptly from a wall-bounded to a free shear flow.
The simplest “complete models” of turbulence are two-equation models in which the solution of two separate transport equations allows the turbulent velocity and length scales to be independently determined. The standard k-e model in FLUENT falls within this class of turbulence model and has become the workhorse of practical engineering flow calculations in the time since it was proposed by Jones and Launder. Robustness, economy, and reasonable accuracy for a wide range of turbulent flows explain its popularity in industrial flow and heat transfer simulations. It is a semi-empirical model, and the derivation of the model equations relies on phenomenological considerations and empiricism.
As the strengths and weaknesses of the standard k-E model have become known, improvements have been made to the model to improve its performance. Two of these variants are available in FLUENT: the RNG k-e model and the realizable k-e model.
Notice:
The term “realizable” means that the model satisfies certain mathematical constraints on the Reynolds stresses, consistent with the physics of turbulent flows. Neither the standard k-E model nor the RNG k-E model is realizable.
An immediate benefit of the realizable k-E model is that it more accurately predicts the spreading rate of both planar and round jets. It is also likely to provide superior performance for flows involving rotation, boundary layers under strong adverse pressure gradients, separation, and recirculation.
The Reynolds stress model (RSM) is the most elaborate turbulence model that FLUENT provides. Abandoning the isotropic eddy-viscosity hypothesis, the RSM closes the Reynolds-averaged Navier-Stokes equations by solving transport equations for the Reynolds stresses, together with an equation for the dissipation rate. This means that four additional transport equations are required in 2D flows and seven additional transport equations must be solved in 3D.
Since the RSM accounts for the effects of streamline curvature, swirl, rotation, and rapid changes in strain rate in a more rigorous manner than one-equation and two-equation models, it has greater potential to give accurate predictions for complex flows. However, the fidelity of RSM predictions is still limited by the closure assumptions employed to model various terms in the exact transport equations for the Reynolds stresses. The modeling of the pressure-strain and dissipation-rate terms is particularly challenging, and often considered to be responsible for compromising the accuracy of RSM predictions.
The RSM might not always yield results that are clearly superior to the simpler models in all classes of flows to warrant the additional computational expense. However, use of the RSM is a must when the flow features of interest are the result of anisotropy in the Reynolds stresses. Among the examples are cyclone flows, highly swirling flows in combustors, rotating flow passages, and the stress-induced secondary flows in ducts.
Successful computations of turbulent flows require some consideration during the mesh generation. Since turbulence (through the spatially varying effective viscosity) plays a dominant role in the transport of mean momentum and other scalars for the majority of complex turbulent flows, you must ascertain that turbulence quantities are properly resolved, if high accuracy is required. Due to the strong interaction of the mean flow and turbulence, the numerical results for turbulent flows tend to be more susceptible to grid dependency than those for laminar flows.
It is therefore recommended that you resolve, with sufficiently fine meshes, the regions where the mean flow changes rapidly and there are shear layers with a large mean rate of strain.
You can check the near-wall mesh by displaying or plotting the values of y+, y*, and Rey, which are all available in the post processing panels. It should be remembered that y+, y*, and Rey are not fixed, geometrical quantities. They are all solution-dependent. For example, when you double the mesh (thereby halving the wall distance), the new y+ does not necessarily become half of the y+ for the original mesh.
For the mesh in the near-wall region, different strategies must be used depending on which near-wall option you are using.
We will describe especially the near-wall mesh guide for the two-layer zonal model, which was the solution selected for our computation.
When you use the two-layer model, the mesh requirements are in terms of y+, not y*:
-When the two-layer zonal model is employed, y+ at the wall-adjacent cell should be, most ideally, on the order of y+ = 1. However, a higher y+ (<5) is acceptable as long as it is well inside the viscous sublayer:
-Most ideally, you should have at least 10 cells within the viscosity-affected near-wall region (Rey < 200) to be able to resolve the mean velocity and turbulent quantities in that region.
Notice for Spalart-Allmaras:
The Spalart-Allmaras model in its complete implementation is a low-Reynolds-number model. This means that it is designed to be used with meshes that properly resolve the viscous-affected region, and damping functions have been built into the model in order to properly attenuate the turbulent viscosity in the viscous sublayer. Therefore, to obtain the full benefit of the Spalart-Allmaras model, the near-wall mesh spacing should be as described in section for the two-layer zonal model.
This will allow the model to solve the equations until the wall, whereas it will automatically use the wall functions if the mesh would be too coarse.
We already know as it was described in the paragraph 2.1.2) and 2.2.2) that the flow over a plate obeys some empirical laws. We will use these laws in order to determine the grid and the size of the plate, which will allow us to observe correctly the phenomena computed by fluent.
Experimentally, we know that the transition from laminar to turbulent flow occurs at a critical value of the Reynolds number Rexcr on the order of 105 to 106 depending on the roughness of the surface and the amount of turbulence in the upstream flow.
We will choose the value of Rexcr =105 to determinate our parameters. This value will be confirms later by the computation.
To determine these parameters we will consider the turbulent boundary layer hypothesis, the same grid will be used to compute the laminar layer in order to make the comparison easier.
If we assume that the critical Reynolds number is approximately at 105, and that the dynamical viscosity of air is n=1.46´105 SI, we can calculate the xtransition and the dtransition from laminar to turbulent flow according to the velocity inlet.


We want both that the phenomena are visible (observable) and that they occurs “in the middle” off our grid.
Flow over a plate:
|
Uo (m.s-1) |
xtransition (mm) |
dtransition (mm) |
|
10 |
146 |
2.3 |
|
5 |
292 |
4.6 |
For Uo=10 m.s-1 the dtransition is a little bit small to be easily observable.
So we will choose a velocity inlet: Uo = 5 m.s-1 and a plate length of 600 mm, so that the transition might occurs in the middle of the box.
Here, we will have to make some simplifying assumptions, because FLUENT is unable to represent an infinite situation…. or it is the case in our computation.
So we will have to make some choices…
The upper and left boundary conditions are set to “pressure outlets”.
The height of the top will be set to 400 mm, which corresponds to 20´ the height of the boundary layer (recommended value).

The upper boundary condition will be set to symmetric. It is important to notice that this boundary condition is an approximation, which doesn’t correspond to reality.
The height of the box will be set to 1200 mm in order to minimize its influence in the computation.
The right edge is set to as an outflow.

To summarize, we will compute a flow with Uo = 5 m.s-1 in a. 2D, 600 mm box, with 2 different heights and boundary conditions.
For both grids we should observe a change to turbulent flow at the middle of the box, with a thickness of approximately 5 mm.
To calculate the thickness of the boundary layer at the end of the box, we will use the turbulent empirical formula, as the flow becomes turbulent after the critical Reynolds number is reached.

We obtain d=19.2 mm at the end of the box.
We have now the dimensions and the parameters of the flow, but to make a good computation with FLUENT, it is also important to make a relevant mesh consideration.
Knowing that we will use the “2 layer zonal model” and whatever turbulent model we are using the grid considerations are almost the same:
- There must be at least 10 lines inside the laminar boundary layer.
-
The “y” size of the cells should be so that the parameter y+= r´(t/r)1/2´y/m is near 1.
(With t wall shear stress).
Following the first idea, we could set the grid so that there are 10 lines in the laminar sublayer. That means in 5mm. In this case near the wall the horizontal lines should be set every 0.5 mm.
Following the second idea, and assuming that the wall shear stress is about 10-2, the cells should have a height of: y = m/(r´(t/r)1/2) = 0.162 mm.
This both approach of grid considerations leads to similar results: the height of the cells should be approximately between 0.1 and 0.5 mm in the boundary layer.
We will build 0.2 mm height cells near the wall.
The height of this “fine” mesh must be at least the thickness of the boundary layer. We will chose a height of 20 mm that corresponds with the height of the turbulent boundary layer at the end of the wall.
The consideration for the horizontal distribution of nodes is less important, however we will put a growth factor for their distribution (starting from the leading edge).
In the rest of the box, a coarser mesh will be used to save computation time.
We have the meshes, the flow parameters, we must now choose a model and the computation will be possible.
In order to test our hypothesis, we will begin with the simple laminar case.
The height of the laminar boundary layer should be 6.6 mm at the end of the wall, and approximately 4.6 mm in the middle of the box.
The velocity inlet is fixed to 5 m.s-1.
The fluid considered is air, it is considered like 2D, laminar, and uncompressible one.
There are no gradient pressure and no heat transfers.
The residuals for continuity are set to 10-5. Lots of computations have been made and have lead to the conclusion that the default convergence parameters ( 10-3) are insufficient for this flow.
Besides, it was often necessary to decrease the relaxation parameters (momentum and turbulence) to obtain a convergence.
By plotting the contours of the velocity with a maximum put to 0.99´5 = 4.95 m.s-1, we can measure the height d of the boundary layer.
The results are gathered is the following tables.
|
Thickness of the BL (mm) |
x=300 |
x=600 |
|
Theoretical (d = 5´(n´x/Uo)1/2) |
4.6 |
6.6 |
|
Computation |
3.6 |
5.4 |
|
Error % |
27 |
22 |

Figure 13: boundary layer at the leading edge

Figure 14: velocity gradient at the end of the plate

Notice:
The distance between 2 lines is 0.2 mm
Figure15: BL thickness at the end of the plate

Figure 16: velocity vectors at the end of the plate.
The velocity gradients near the wall are quite small.

Outside the boundary layer the velocity gradients are smaller.
Figure 17: velocity field outside the boundary layer
|
Thickness of the BL (mm) |
x=300 |
x=600 |
|
Theoretical (d = 5´(n´x/Uo)1/2) |
4.6 |
6.6 |
|
Computation |
3.8 |
5.2 |
|
Error % |
21 |
21 |


Figure 18: BL thickness at the end of the plate figure 19: velocity distribution outside the BL
Even with my simple grid it was difficult to make the computation converge… we can hardly reach the value of 10-5 for the residuals - even if it is necessary to obtain satisfactory results -.
The both computations and results are almost the same. The average error in the thickness of the boundary layer is 22%.
This difference between the analytical model - which comes maybe from the boundary conditions or from a bad convergence - is quite significant.
To deal with this problem, many computations have been done with different grids and parameters. Sometimes with finer meshes the convergence was better, but the error was still in the same scale…
Outside the boundary layer, the velocity gradients are smaller. The speed vary between 4.95 and 5.15 m.s-1 with 80% of the between 4.99 and 5.05 m.s-1 (Fig 17&19).
Fig 14&16 illustrate the velocity gradients and the velocity vectors at the end of the plate. We can notice the velocity grows slowly producing strong small gradients, and also the particular shape of the velocity field, which will be interesting to compare with the turbulent one.
The velocity inlet is fixed to 5 m.s-1. The turbulence parameters settings are:
- Turbulence intensity 3%, which is representing a low turbulence at the velocity inlet.
- Turbulence scale is set to 8 mm, following the Fluent guide recommendation for wall-bounded flows, which is: l =0.4´d (where d is the thickness of the boundary layer).
The fluid considered is air, it is considered like a 2D, turbulent, uncompressible flow.
There are no gradient pressure and no heat transfers.
The residual for convergence are set to 10-5 when it is possible!!!!
We will so test successively the 3 models: Spalart-Allmaras, k-e, and the Reynolds stress model, and compare the results with the theoretical ones.
First, it is important to notice that the mesh should be fine enough so that the boundary layer will be computed instead of using the wall functions…which are used in this model when the mesh is to coarse (y+ << 30).
|
Thickness of the BL (mm) |
x=300 (d =5´ (n´x/U)1/2 |
x=600 (0.370´(n/U)1/5 ´ x4/5) |
|
Theoretical |
4.6 |
19.2 |
|
Computation |
11.6 |
23.8 |
|
Error % |
150!!! |
24 |

Figure 20: global shape of BL

<==== Theoretical thickness
In this computation the thickness of the boundary layer is bigger than the theoretical one!!!!
Figure 21: thickness of BL at the end of the plate

Figure 22: velocity vectors at the end of the plate
Contrary to the laminar computation, the near wall gradients are stronger. But the global profile is flatter. Besides the turbulent boundary layer is thicker.

This model was quite hard to converge…
Even if we reached good residual values, this irregular velocity field outside the BL seems to indicate that the convergence is not excellent.
Figure 23: velocity field outside the boundary layer
|
Thickness of the BL (mm) |
x=300 (d =5´ (n´x/U)1/2 |
x=600 (0.370´(n/U)1/5 ´ x4/5) |
|
Theoretical |
4.6 |
19.2 |
|
Computation |
8.4 |
17.6 |
|
Error % |
82!!! |
9 |
Like the laminar case, we can notice that the difference between the empirical solution and the computation is huge…
However, the error is decreasing along the wall…
The difference can be observed in the shape of the velocity too. Indeed, in the computed velocity field, we cannot observe the “bump” which should normally appear with the turbulence. The computed shape grows more regularly and constantly.


Figure 24: BL at the leading edge figure 25: velocity vectors at the leading edge

Figure 26: velocity field at the end of the plate

figure 27:thickness of BL at the end of the plate
Fig27: On this picture, we can notice that the computation corresponds very well to the analytical prediction.

Figure 28: velocity vectors at the end of the plate
Like the Spalart-Allmaras model we can notice the large gradient of velocity neat the wall, and a flat profile in the upper par.

Figure 29: global shape of the BL

Figure 30: velocity field outside the BL

Figure 31: Rey < 200 number (thickness of the laminar sublayer)
Here, we can observe an interesting reduction of the thickness of the viscous sub-layer, where the turbulence should start. It means that in the boundary layer (Rex » 105 = Rexcr, as we discussed section 3.2.1), the viscous effects become less important in comparison to the turbulent effects. It confirms that something is happening in the middle of the box, where the Rexcr is reached.

Figure 32: Rex number
It is interesting to notice that the brutal decrease of the laminar boundary layer fig31) occurs between the Rex =1 and 1.25 *10^5. It confirms, “something is happening” at the Rexcr value.
Indeed, we constructed to box attempting to make the turbulent transition occur in the middle of the box. And even if we are not able to observe the “bump”, this brutal decrease of the laminar sublayer thickness means that to the transition occurs.
It was impossible to make this model “really” converge, even with very low relaxation parameters. However I reached the value of 10-5 for the residuals (after 23000 iterations!!!), with quite stable quantities… meaning that the better accuracy might be reached.
|
Thickness of the BL (mm) |
x=300 (d =5´ (n´x/U)1/2 |
x=600 (0.370´(n/U)1/5 ´ x4/5) |
|
Theoretical |
4.6 |
19.2 |
|
Computation |
/ |
24 |
|
Error % |
/ |
25 |


Figure 33: global shape of BL figure 34: velocity field outside the boundary layer


Figure 35: velocity field at the end of the plate figure 36: thickness of the BL at the end of the plate
Fig36 like the Spalart-Allmaras model, this one computes a BL thicker than the prevision...

Figure 37:velocity vectors at the end of the plat
Here the gradient near the wall are a little bit smaller than the 2 precedent models...
But this velocity field is not as good as the 2 others.

Figure 38: Rey <200 number
Difficult to deduce anything from this picture, as the irregular shape shows a convergence problem... but we can still guess that something is happening with he Rey number!
With this model it was impossible to make the computation converge…
|
Thickness of the BL (mm) |
x=300 (d =5´ (n´x/U)1/2 |
x=600 (0.370´(n/U)1/5 ´ x4/5) |
|
Theoretical |
4.6 |
19.2 |
|
Computation |
9.6 |
9.2 |
|
Error % |
100 |
52 |


Figure 39: thickness of the BL at the end of the plate figure 40: velocity field outside the BL
Fig40 seems to indicate a bad convergence...


Figure 41: global shape of the BL figure 42: Rey < 200 number
Fig42 shows that contrary to the first grid results, there is a decrease of the boundary layer in the middle of the box...However we will see that the velocity profile is different from the laminar one fig43.

Figure 43: velocity vectors at the end of the plate
Even if we cannot observe the brutal decrease of the laminar sublayer, the velocity profile at the end of the plate is quite good (large gradient near the wall and a flat profile above).
With this computation too, it was impossible to reached a real convergence, we hardly get 10-4 for the residuals after 7000 iterations…
|
Thickness of the BL (mm) |
x=300 (d =5´ (n´x/U)1/2 |
x=600 (0.370´(n/U)1/5 ´ x4/5) |
|
Theoretical |
4.6 |
19.2 |
|
Computation |
12.8 |
9 |
|
Error % |
180 |
53 |


Figure 44: global shape of BL figure 45: velocity field outside the BL


Figure 46: thickness of BL at the end of the plate figure 47: zoom in the middle box

This computation lacks obviously of convergence…
Figure 48: zoom on the Rey < 200 number near the leading edge

Figure 49: velocity vectors at the end of the plate
Nothing can be really deduce of this computation...Even the velocity profile do not seem good and suffers obviously from a lack of convergence...
All these computations gave different results, however we can draw some interesting conclusions:
-Whatever the model or the grid we are using, the thickness error between the analytical results and the computation is approximately at 20% for the laminar computation.
It can drop to 10% for a fully developed turbulent computation, however the thickness of the turbulent boundary layer is not accurate during the transition region… along this zone the error can exceed 100%!
-Making a turbulent computation, Even if the fully developed turbulent region is well restored (good thickness and a good velocity field), it is impossible to observe the “bump” that should appear when the flow become turbulent.
The boundary layer grows regularly to reach the theoretical thickness, but there is no brutal change in the velocity field as we could expect. Refer to figures: 20,29, 33…
-However, it is possible to see the reduction of thickness of the laminar sublayer when the flow should start to be turbulent (Rex= 100000 or Rey>200). Refer to figures: 31, 32, 38, and 48.
-The model, which gave the best results both for the convergence and the accuracy, was the k-e model.


I make a point of thanking all the “fluid mechanics department” research team, which have accommodated me and supported me and help throughout this training course.
I also more particularly wish thanking my tutor Millan Schuster like Richard Mattas who did their utmost to make my stay most pleasant possible from their availability and their great attention in my connection.
Moreover, I wish to thank the University of Plzen and particularly Marketa Chechurova, which provided us quickly an accommodation and which helped us in all our " administrative " steps.
FLUENT USER’S GUIDE:
Fluent Incorporated (1998)
FLUID DYNAMICS:
W.F Hughes & J.A Brighten – Mc Graw Book Company (1967)
FUNDAMENTALS OF FLUID MECHANICS:
B.R Munson, D.F Young &T.H Okiishi – John Wiley & Sons (1998)